A matemática da epidemia

A epidemia do corona vírus está causando milhares de mortes ao redor do mundo. A situação é extremamente preocupante em países como China, Irã, Itália e Espanha.

No Brasil, até o momento, não existem mortes registradas. Até agora (13 de março) são 98 casos confirmados de infectados e cerca de 1500 casos estão sendo investigados. Autoridades sérias são unânimes em afirmar que o número de casos vai crescer muito.

O que é este "muito"? Como quantificar isto? Como a matemática pode ajudar a entender isto?

Existe uma área de pesquisa, chamada de epidemiologia matemática, que estuda exatamente este tipo de problema. Esta não é minha área de pesquisa, mas como em geral os modelos epidemiológicos fazem uso de equações diferenciais, vou me meter um pouco no assunto. Além disto, como as aulas presenciais foram suspensas pela Unicamp e eu prometi para meus alunos que iria mantê-los ocupados com atividades online, nada melhor do que fazer algumas contas com equações diferenciais aplicadas à nossa ordem do dia.

Obviamente isto aqui não é um artigo científico, e o objetivo é simplesmente matematizar algumas características do problema. No final existem algumas referências bibliográficas com análises mais profundas, inclusive do ponto de vista estatístico. Uma análise muito bem feita sobre a situação na Itália está neste artigo.

Nosso modelo epidemiológico

Iremos utilizar um modelo tradicional para estudar a propagação de doenças que são causadas por vírus ou bactérias: as equações SIR. As letras vem de Suscetíveis, Infectados e Recuperados. Neste artigo as equações SIR foram utilizadas para modelar com bastante sucesso a evolução de uma epidemia de gripe que atingiu os EUA nos anos de 1968 e 1969 e ficou conhecida como gripe de Hong Kong.

As equações SIR dividem a população total em três grupos: os que ainda não foram infectados (S), os que estão infectados (I), e aqueles que foram infectados e já se recuperaram (R). O grupo dos infectados é que de fato tem a capacidade de transmitir a doença. Cada população evolui com o tempo, portanto estes valores são funções de $t$: $S(t)$, $I(t)$ e $R(t)$.

Ao invés de usar números absolutos da população, será mais simples considerar as funções normalizadas. Se $N$ é o total da população, vamos considerar as funções $s(t)=S(t)/N$, $i(t)=I(t)/N$ e $r(t)=R(t)/N$. Note que enquanto $S(t)+I(t)+R(t)=N$, estas novas funções satisfazem $s(t)+i(t)+r(t)=1$ para qualquer valor de $t$.

Equações

Veremos agora quais equações descrevem a evolução de cada uma destas populações.

Vamos assumir que a população suscetível não aumenta ou diminui devido a fatores externos (mortes e/ou nascimentos), mas só pela infecção. Isto não é totalmente verdade, mas esta hipótese simplifica o modelo.

A quantidade $s(t)$ de indivíduos suscetíveis diminui: no começo ela é igual à população toda, e a medida que pessoas são infectadas, $i(t)$ e $r(t)$ aumentam e portanto $s(t)$ precisa diminuir. A variação depende basicamente de quantas pessoas sadias cada infectado consegue contaminar por dia, e vamos denotar este valor por $c$: o fator de contaminação. Apesar do nosso modelo ser em tempo contínuo, em geral vamos considerar unidades pequenas de tempo $t$. Assim, cada infectado contamina em média $c\cdot s(t)$ pessoas por dia. Como são $I(t)$ infectados no dia $t$, a variação no número de indivíduos suscetíveis é de $S'(t)=-c s(t) I(t)$. Dividindo esta equação por $N$ obtemos nossa primeira equação diferencial: $s'(t)=-cs(t)i(t)$. Inicialmente temos $s(0)=1$ (ou, de forma equivalente, $S(0)=N$).

A constante que estamos denotando por $c$ em geral é denotada por $R_0$ e chamada de R naught (mais detalhes aqui). Estimativas recentes para o $R_0$ no caso do coronavírus indicam o valor de $R_0=2,2$, ou seja, em média uma pessoa infectada irá contaminar outras 2,2 pessoas. No caso do sarampo, por exemplo, este número é maior do que 10.

Deduzir a equação que descreve a variação da população de recuperados é fácil. Uma fração de pessoas, que vamos denotar por $b$ (taxa com a qual as pessoas ficam boas), se recupera a cada dia, e esta é uma fração do número de infectados. Além disto, a função $r(t)$ aumenta a cada dia. A variação desta população é dada por $r'(t)=b i(t)$, sendo a condição inicial $r(0)=0$ (no começo não existem indivíduos recuperados).

Para deduzir a equação que descreve a evolução da população de infectados, vamos partir de uma hipótese bastante razoável: a soma das variações das populações é nula. Ou seja, os indivíduo trocam de "grupos", sem acréscimo ou diminuição da população total (pessoas vão morrer, mas não vamos tirá-las da população total). Ou seja, num dia $t$ qualquer, teremos $s'(t)+i'(t)+r'(t)=0$. Sendo assim, obtemos a equação para descrever a evolução da população de indivíduos recuperados: $i'(t)=-s'(t)-r'(t)=cs(t)i(t)-bi(t)$.

Qual deve ser o valor de $i(0)$, ou seja, o número inicial de indivíduos infectados? Bom, alguém sempre é o chamado "paciente zero". Se começarmos com $i(0)=0$, então $i(t)$ será zero sempre. Iremos considerar que uma certa quantidade de pacientes infectados foi inserida na população, digamos $I(0)=d$, de doentes iniciais ($d$ é pequeno em relação à população $N$).

Chegamos finalmente ao nosso sistema de equações diferenciais, com suas condições iniciais (nosso PVI - problema de valor inicial):

$$\begin{array}{l}
s'(t)=-c\cdot s(t)\cdot i(t),\\
r'(t)=b \cdot i(t), \\
i'(t)=c\cdot s(t)\cdot i(t)-b\cdot i(t),\\
s(0)=1, \ r(0)=0, \ i(0)=d/N,
\end{array}
$$

lembrando que $c$ é o fator de contaminação (quantas pessoas um infectado contamina, em média), $b$ é a taxa com que as pessoas ficam boas, $d$ é o número inicial de doentes (doentes que são inseridos na população) e $N$ é a população total (pode-se pensar o fator $d/N$ como sendo uma única constante).

Este é um sistema de equações diferenciais não-lineares de primeira ordem. Este sistema não tem solução explícita, e seu estudo utilizando os métodos da teoria qualitativa dos sistemas dinâmicos é prejudicado (tecnicamente: a parte linear do sistema tem autovalores nulos). Vamos usar o Mathematica para ver como são as soluções, principalmente o gráfico de $i(t)$, que descreve como será a evolução do número de infectados.

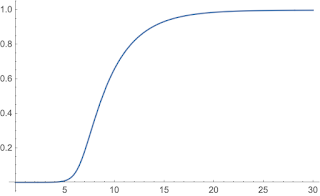
Iremos usar $c=2,2$ (o que parece indicar a literatura médica sobre o caso atual), $b=1/3$ (valor comum em viroses) e $d=5$ (supondo 5 pacientes introduzidos numa população de 1 milhão de pessoas). O gráfico de $i(t)$ está na figura abaixo. Note que existe um pico de infectados, afetando quase metade da população, em pouco tempo.

O gráfico de $s(t)$, que mostra a evolução da população suscetível, está abaixo. Como esperado, ela começa bem grande e diminui rapidamente, até não existir quase ninguém suscetível ao contágio (quando quase todos já tiverem sido infectados).

O número de recuperados também tem crescimento rápido, como pode ser visto no gráfico de $r(t)$ abaixo. Este modelo só funciona para vírus de baixa letalidade, cujas mortes não tem grande impacto na ordem de magnitude da população original.

O primeiro gráfico foi feito considerando o valor de 2.2 para o R naught. Agora imagine que cada pessoas infectada não consiga contaminar tantas pessoas (por exemplo, tomando ações de quarentena, como por exemplo a suspensão de aulas e eventos, e isolando os doentes), e em média cada pessoa só consiga infectar no máximo uma pessoa. Neste caso o gráfico de $i(t)$ seria como abaixo.

Perceba que o percentual máximo de infectados diminui drasticamente (cai pela metade), e, além disto, leva-se mais tempo para atingir o máximo (por exemplo, permitindo aos sistemas de saúde que se preparem melhor para os atendimentos).

Conclusões

Enfim, o fato é que o número de infectados vai aumentar bastante de agora até o momento em que atingiremos o pico dos infectados, e depois disto irá diminuir. O importante é tomarmos medidas que evitem aglomerações, diminuindo o R naught, ainda que de forma forçada.

Se você não entendeu bem a matemática deste texto, dê mais uma chance para o gráfico abaixo. A curva em azul é o número de infectados com o R naught de 2.2, ou seja, sem medidas de quarentena. A curva vermelha é o número de infectados considerando o uso de medidas de quarentena.

Note que medidas de quarentena diminuem muito o pico da curva. Ou seja, boa parte de nós será infectado  em algum momento, só não podemos ficar todos doentes no mesmo momento, ou o sistema de saúde entrará em colapso. Este texto trata disto e recomendo sua leitura.

Bônus

Mencionei que o índice R naught do sarampo é de aproximadamente 10. O que aconteceria com uma população sem vacina que fosse exposta ao sarampo? Este seria o gráfico de $i(t)$ para este caso:

Percebe-se um contágio muito mais rápido e atingindo 90% da população. Ou seja: o covid-19 é preocupante, mas muito mais preocupante são os movimentos obscurantistas como o anti-vacinas. Veja bem, terraplanismo também é uma loucura, mas pelo menos não dizimaria uma população (a curto prazo)..

Resumindo: lavem as mãos, sempre vacinem as crianças e não espirrem nos amigos! Só assim você estará contribuindo para a manutenção da raça humana aqui na Terra (seja ou não isto uma boa ideia..). Veja mais informações nesta página da Unicamp e também nesta página do CECOM/Unicamp.

Ps.: Versão atualizada com base em sugestões da Profa. Laura Rifo, Giovani Nascimento, Rita Santos, Leo Barichello e outros que eu devo ter esquecido. Obrigado por terem lido com detalhes!

Referências bibliográficas

1. Robert Peckham, COVID-19 and the anti-lessons of history, The Lancet.

2. https://www.maa.org/press/periodicals/loci/joma/the-sir-model-for-spread-of-disease-introduction

3. https://www.healthline.com/health/r-nought-reproduction-number

4. https://www.ncbi.nlm.nih.gov/books/NBK554776/

5. https://towardsdatascience.com/covid-19-infection-in-italy-mathematical-models-and-predictions-7784b4d7dd8d?gi=38d86e59ec06

6. https://www.iflscience.com/health-and-medicine/why-its-crucial-to-flatten-the-curve-to-help-contain-covid19/